Today’s Modeling and Control blog post, PID Feedback Control, by Emerson’s Terry Blevins, describes the impact unmeasured disturbances can have on a process. Trying to manually control these disturbances is difficult, given the increasing complexity of process manufacturing facilities. Proportional-Integral-Derivative (PID) control has been the principal means to automatically control these disturbances. Terry writes:
Even though PID control has been used since before the introduction of process control systems, efforts to provide better techniques for feedback control have gained only limited acceptance. Over the years the PID algorithm has proven to be applicable to a wide variety of process applications for the implementation of feedback control and remains the heart of control systems today.
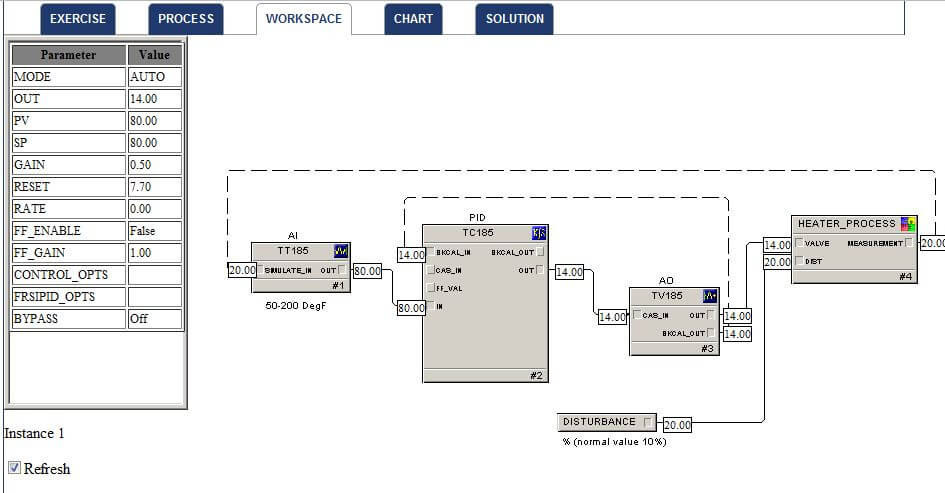
He points to an exercise on the Control Loop Foundation website, PID Feedback Control, to show the impact of disturbances in manual and automatic modes, and the impact with changes in the PID controller gain settings. The workshop includes a series of steps to perform, the process P&ID, the workspace where the simulation runs and changes are made, the trend chart showing the impact of these changes, and a solution video describing this exercise in detail.
In the spirit of, “It’s so easy a blogger can do it”, I gave it a whirl. Here are the steps from the exercise:
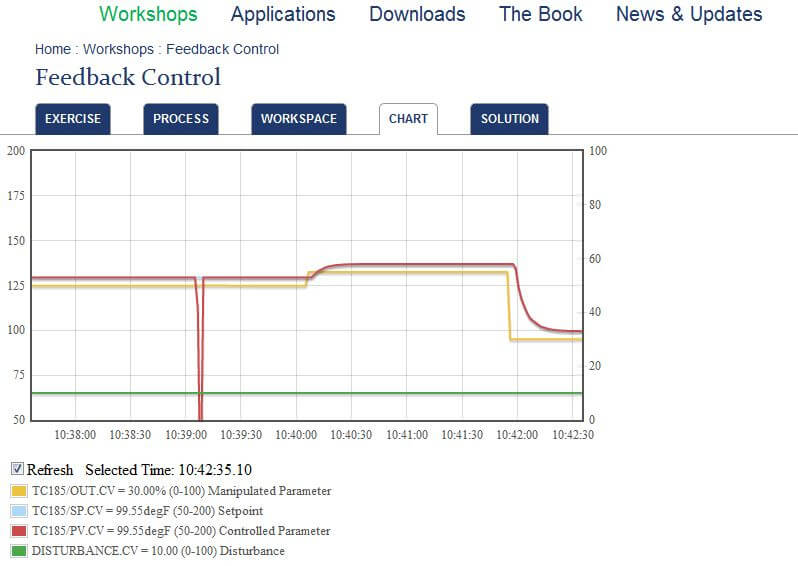
- Step 1. In the feedback control workspace, set the mode of the PID to Manual using the MODE parameter. Change the PID output using the OUT parameter and observer the process response.
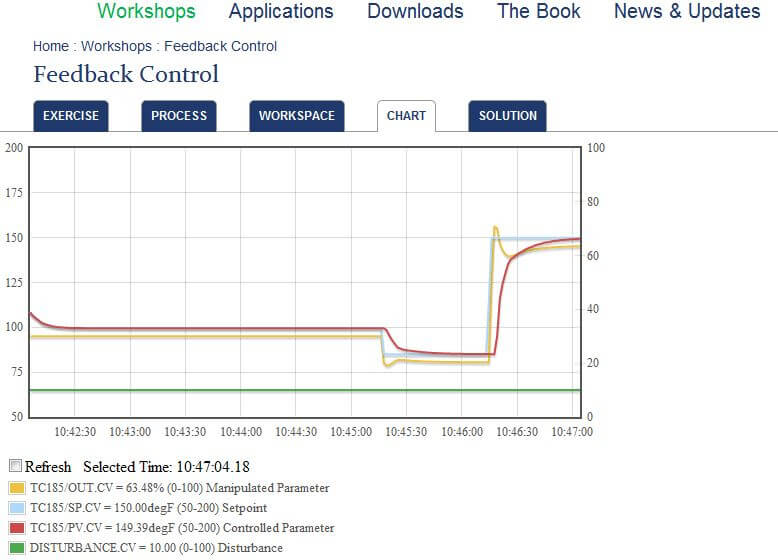
- Step 2. Set the PID mode to Auto and change the setpoint using the SP parameter. Observe the process response.
- Step 3. Introduce an unmeasured process disturbance by changing the DISTURBANCE input. Observe the impact on the process and the action taken by the PID block to return the temperature to its setpoint.
- Step 4. Reduce the PID GAIN by a factor of 2, then repeat steps 2 and 3. Observe the impact of the gain change on the response to setpoint and disturbance changes.
Here’s the process I was playing with:
Here’s the chart following step 1’s change of PID output:
Here’s step 2 with the PID loop back in automatic mode with a setpoint (SP) bump:
Here’s step 3 with a couple of changes in the disturbance variable (thankfully, this is not a real plant!):
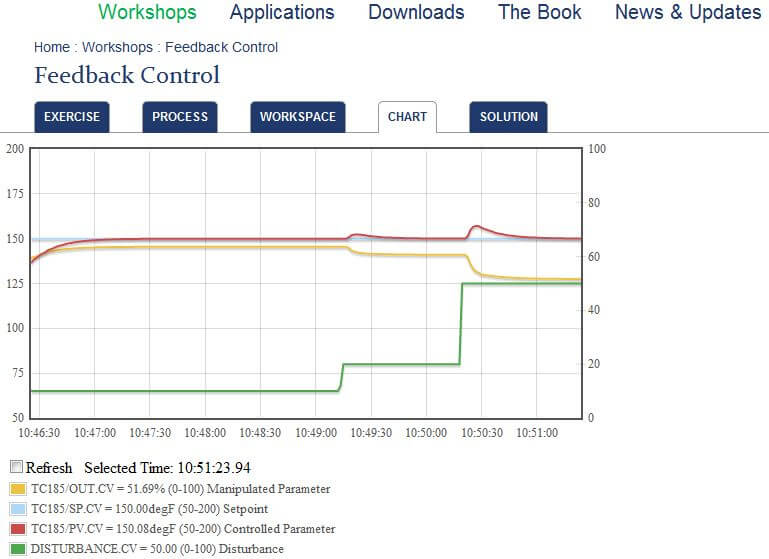
Finally, here’s step 4 when I halved the PID loop gain and bumped the disturbance variable. See how much longer the process variable (PV – red line in trend chart) takes to reach the new setpoint?
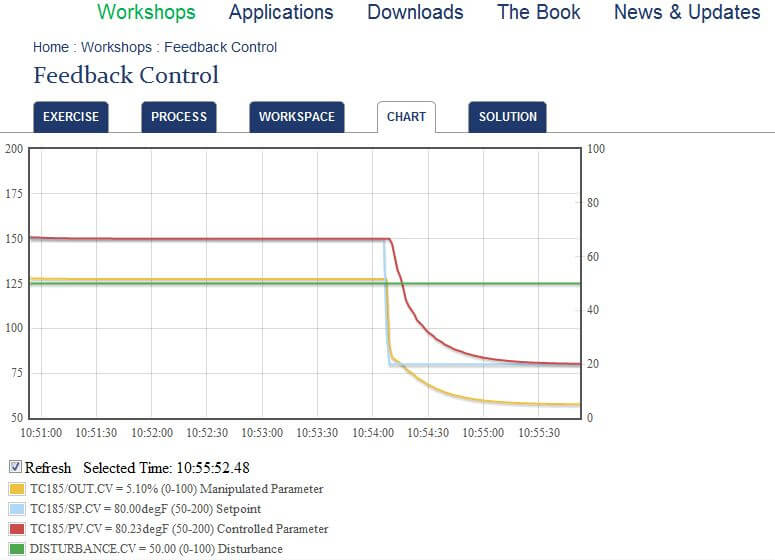
I thought I’d share a couple screen captures to show how easy it is to manipulate the workspace and see the effects of disturbances and tuning on the simulated process. Give it a try.
Also, check out some of the other exercises, and consider getting your hands on Terry and team’s, Control Loop Foundation – Batch and Continuous Processes book–from which these exercises are derived.
